ΚΟΙΝΗ ΕΦΑΠΤΟΜΕΝΗ ΔΥΟ ΠΑΡΑΣΤΑΣΕΩΝ ΣΕ ΜΗ ΚΟΙΝΟ ΣΗΜΕΙΟ

Rendered by QuickLaTeX.com

Έστω η ευθεια $(\epsilon):y =\lambda x +\beta$ η κοινη εφαπτομενη των $C_{f}$ και $C_{g}$ στα σημεία $A(x_1,f(x_{1}))$ και $B(x_{2},g(x_{2}))$ αντίστοιχα.

Τότε για τον συντελεστή διεύθυνσης (κλίση ) της ευθείας θα ισχύει: $\lambda_{\epsilon}=f'(x_{1})$ και $\lambda_{\epsilon}=g'(x_{2})$
οπότε παίρνουμε:

$f'(x_{1})=g'(x_{2}).$

Επισης για το σημείο $A( x_{1},f(x_{1}))$ της $C_{f}$ έχουμε οτι ανήκει και στην ευθεία $(\epsilon)$ οπότε

$\begin{align*} A( x_{1},f(x_{1})) \in (\epsilon): y & =\lambda x +\beta \Rightarrow \\\\ f(x_{1}) & = \lambda x_{1} + \beta \xRightarrow[\text{}]{\lambda =f'(x_{1})} \\\\ f(x_{1}) & = f'(x_{1})\cdot x_{1} + \beta \quad (1) \end{align*}$

Aλλά και το σημείο $B( x_{2},g(x_{2}))$ της $C_{g}$ έχουμε οτι ανήκει και στην ευθεία $(\epsilon)$ οπότε

$\begin{align*} B( x_{2},g(x_{2})) \in (\epsilon): y & =\lambda x +\beta \Rightarrow \\\\ g(x_{2}) & = \lambda x_{2} + \beta \xRightarrow[\text{}]{\lambda =g'(x_{2})} \\\\ g(x_{2}) & = g'(x_{2})\cdot x_{2} + \beta \Rightarrow \\ g(x_{2}) & -g'(x_{2})\cdot x_{2} = \beta\Rightarrow \\ \beta & =g(x_{2}) -g'(x_{2})\cdot x_{2} \quad (2) \end{align*}$

Αντικαθιστώντας το $\beta$ στην σχέση (1) έχουμε:

$\begin{align*} (1)\xRightarrow[\text{}]{(2)}f(x_{1}) = & f'(x_{1})\cdot x_{1} + g(x_{2}) -g'(x_{2})\cdot x_{2}\Rightarrow\\\\ f(x_{1})-&f'(x_{1})\cdot x_{1} = g(x_{2}) -g'(x_{2})\cdot x_{2} \Rightarrow\\\\ f'(x_{1})&\cdot x_{1}-f(x_{1}) = g'(x_{2})\cdot x_{2}- g(x_{2}). \end{align*}$

Ανακεφαλαιώνοντας:
Για να βρούμε την κοινη εφαπτομενη των $C_{f}$ και $C_{g},$ δύο παραγωγίσιμων συναρτήσεων $f,g:A\to \rr,$ στα σημεία $A(x_1,f(x_{1}))$ και $B(x_{2},g(x_{2})).$
Θα πρέπει:

$f'(x_{1})=g'(x_{2}).$

$f'(x_{1})&\cdot x_{1}-f(x_{1}) = g'(x_{2})\cdot x_{2}- g(x_{2}).$

Rendered by QuickLaTeX.com

Λύση
Οι συναρτήσεις $f(x)= x^{2}+1$ και $g(x)=2x^{2}+2x ,$ είναι παραγωγίσιμες στο $\rr,$ με $f'(x)=2x$ και $g'(x)= 4x+2,$ αντίστοιχα.
Για να βρούμε την κοινη εφαπτομενη των $C_{f}$ και $C_{g},$
θα πρέπει:

$f'(x_{1})=g'(x_{2} )\Rightarrow 2x_{1}=4x_{2}+2\Rightarrow x_{1}=2x_{2}+1\quad (1).$

και

$\begin{align*} &f'(x_{1})\cdot x_{1}-f(x_{1}) = g'(x_{2})\cdot x_{2}- g(x_{2})\Rightarrow\\\\ &2x_{1}\cdot x_{1}-(x_{1}^{2}+1) =(4x_{2}+2)\cdot x_{2}-(2x_{2}^{2}+2x_{2}) \Rightarrow\\\\ &2x_{1}^{2}-x_{1}^{2}-1=4x_{2}^{2}+2x_{2}-2x_{2}^{2}-2x_{2} \Rightarrow\\\\ &x_{1}^{2}-1=2x_{2}^{2}\xRightarrow[\text{}]{(1)} \\\\ &(2x_{2}+1)^{2}-1=2x_{2}^{2}\Rightarrow\\\\ &4x_{2}^{2}+4x_{2}+1-1=2x_{2}^{2}\Rightarrow\\\\ &4x_{2}^{2}+4x_{2}=2x_{2}^{2}\Rightarrow\\\\ &4x_{2}^{2}+4x_{2}-2x_{2}^{2}=0\Rightarrow\\\\ &2x_{2}^{2}+4x_{2}=0\Rightarrow\\\\ &2x_{2}\cdot(x_{2}+2)=0\Rightarrow\begin{cases} x_{2}=0\\ \quad \text{ή} \\ x_{2}=-2 \end{cases} \end{align*}$

Για την έυρεση του $x_{1}$ διακρίνουμε δύο περιπτώσεις έχουμε:
Περίπτωση.1
Για $x_{2}=0$
$(1): x_{1}= 2\cdot x_{2}+1\Rightarrow x_{1}= 2\cdot 0 +1 \Rightarrow x_{1}=1.$
Επιπλέον:
Επειδη $A(x_{1},f(x_{1}))$ τότε $A(1,f(1))$
με $f(x)= x^{2}+1\xRightarrow[\text{}]{x_{1} =1} f(1) = 1^{2}+1 \Rightarrow f(1) =2.$
άρα $Α(1,1)$

Επίσης
Επειδή $B(x_{2},g(x_{2})) \text { για } \quad x_{2} =0$ έχουμε $B(0, g(0))$
με $g(x)= 2x^{2}+2x\xRightarrow[\text{}]{x_{2} = 0} g(0) = 2\cdot 0^{2}+2\cdot 0 \Rightarrow g(0) =0.$
δηλαδή η $C_g$ για $x_{2} =0$ διέρχται από την αρχή τον αξόνων $O(0,0)$
Εύκολα βλέπουμε ότι η $C_{f}$ στο σημείο της $A(1,1)$ έχει κοινή εφαπτομένη με την $C_{g}$ στο σημειο της $O(0,0)$
αφού:

$\begin{align*} & (\epsilon): y -f(1) =f'(1)(x-1) \\ &\text{με} \quad f'(x) = 2x \xRightarrow[\text{}]{x = 1} f'(1)= 2\quad \text {οπότε} \\ & (\epsilon): y -2 =2 (x-1)\Rightarrow \\ & (\epsilon): y-2= 2x-2\Rightarrow \\ & (\epsilon): y= 2x-2+2\Rightarrow \\ & (\epsilon): y=2x. \end{align*}$

επίσης

$\begin{align*} & (\epsilon): y -g(0) =g'(0)(x-1) \\ &\text{με} \quad g'(x) = 4x+2 \xRightarrow[\text{}]{x = 0} g'(0)= 2\quad \text {οπότε} \\ & (\epsilon): y -0 =2 (x-0)\Rightarrow \\ & (\epsilon): y=2x. \end{align*}$

Rendered by QuickLaTeX.com

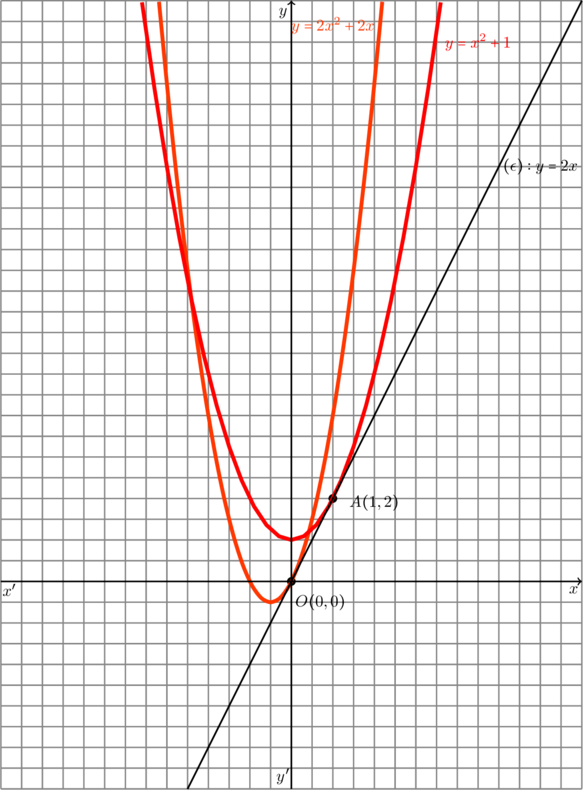
Περίπτωση.2 Για $x_{2}=-2$
$(1): x_{1}= 2\cdot x_{2}+1\Rightarrow x_{1}= 2\cdot (-2) +1 \Rightarrow x_{1}=-3.$
Επιπλέον:
Επειδη $\Gamma(x_{1},f(x_{1}))$ τότε $\Gamma(-3,f(-3))$
με $f(x)= x^{2}+1\xRightarrow[\text{}]{x_{1} =-3} f(-3) = (-3)^{2}+1 \Rightarrow f(-3) =10.$
άρα $\Gamma(-3,10)$

Επίσης
Επειδή $\Delta(x_{2},g(x_{2})) \text { για } \quad x_{2} =-2$ έχουμε $\Delta(-2, g(-2))$
με $g(x)= 2x^{2}+2x\xRightarrow[\text{}]{x_{2} = -2} g(-2) = 2\cdot (-2)^{2}+2\cdot (-2) \Rightarrow$

$g(-2) =2\cdot 4 +2\cdot (-2)\Rightarrow g(-2) =8 -4\Rightarrow g(-2)=4.$

άρα $\Delta(-2,4)$

Επιπλέον $f'(x) = 2x \xRightarrow[\text{}]{x = -3} f'(-3)= -6$
και $g'(x) = 4x+2 \xRightarrow[\text{}]{x = -2} g'(-2)= 4\cdot(-2) +2 \Rightarrow g'(-2)=-6.$

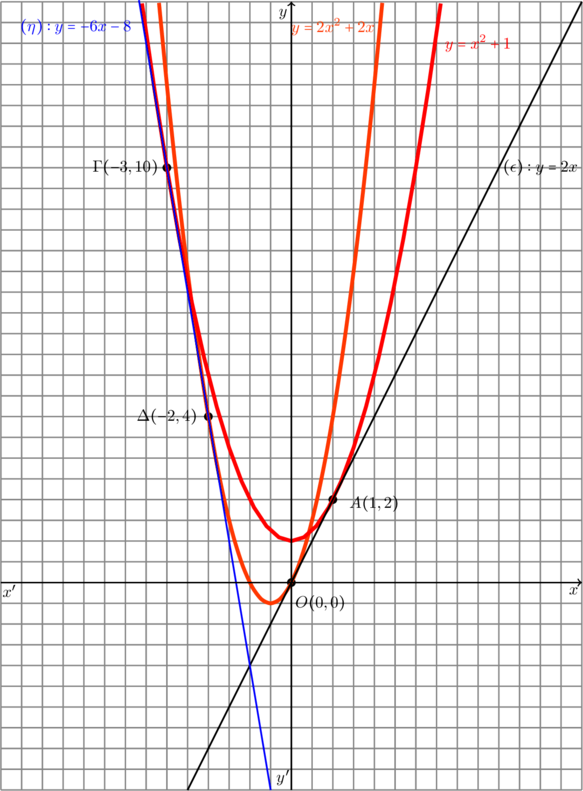
Εύκολα βλέπουμε ότι η $C_{f}$ στο σημείο της $\Gamma(-3,10)$ έχει κοινή εφαπτομένη με την $C_{g}$ στο σημειο της $\Delta(-2,4)$
αφού:

$\begin{align*} & (\eta): y -f( -3) =f'( -3)(x +3) \\ &\text{με} \quad f'(x) = 2x \xRightarrow[\text{}]{x = -3} f'( -3)= -6, \\ &\quad \text {οπότε:}\\ & (\eta): y -10 =-6 (x+3)\Rightarrow \\ & (\eta): y-10= -6x-18\Rightarrow \\ & (\eta): y= -6x-18+10\Rightarrow \\ & (\eta): y= -6x-8. \end{align*}$

επίσης

$\begin{align*} & (\eta): y -g(-2) =g'(-2)(x+2) \\ &\text{με} \quad g'(x) = 4x+2 \xRightarrow[\text{}]{x = -2} g'(-2)= 4\cdot(-2)+2\Rightarrow \\ &g'(-2)=-6,\quad \text {οπότε:}\\ & (\eta): y -4 =-6 (x+2)\Rightarrow \\ & (\eta): y-4=-6x-12\Rightarrow \\ & (\eta): y=-6x-12+4\Rightarrow \\ & (\eta): y= -6x-8. \end{align*}$

Rendered by QuickLaTeX.com

Βιβλιογραφία: Μπάρλας, αυτόεκδοση.

Αυτή η εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή 4.0 Διεθνές .

Ένας ιστότοπος για τα Μαθηματικά

Δ	Τ	Τ	Π	Π	Σ	Κ
						1
2	3	4	5	6	7	8
9	10	11	12	13	14	15
16	17	18	19	20	21	22
23	24	25	26	27	28	29
30	31

Ν. Α. Διακόπουλος

ΚΟΙΝΗ ΕΦΑΠΤΟΜΕΝΗ ΓΡΑΦΙΚΩΝ ΠΑΡΑΣΤΑΣΕΩΝ ΣΕ ΜΗ ΚΟΙΝΟ ΤΟΥΣ ΣΗΜΕΙΟ

Αφήστε μια απάντηση Ακύρωση απάντησης

Ένας ιστότοπος για τα Μαθηματικά