Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ

ΔΙΑΝΥΣΜΑΤΙΚΗ ΑΚΤΙΝΑ ΚΑΙ ΔΙΑΝΥΣΜΑΤΙΚΗ ΑΚΤΙΝΑ ΜΕΣΟΥ

Σχολιάστε
Print Friendly, PDF & Email

Οι περισσότερες ασκήσεις με διανυσματικές σχέσεις μπορούν να λυθούν με τη μέθοδο των διανυσματικών ακτίνων.

  • Όταν θέλω πρόσθεση έχω το ίδιο μεσαίο σημείο

        \[\overrightarrow{AB} = \overrightarrow{AO} +\overrightarrow{OB}\]

  • Όταν θέλω αφαίρεση έχω το ίδιο αρχικό σημείο

        \[\overrightarrow{AB} = \overrightarrow{OA} -\overrightarrow{OB}\]

    Δηλαδή όταν ένα διάνυσμα πρέπει να αναλυθεί:

    σε άθροισμα, το γράφω \overrightarrow{AB} = \overrightarrow{AO} +\overrightarrow{OB}
    σε διαφορά, το γράφω \overrightarrow{AB} = \overrightarrow{OA} -\overrightarrow{OB}

  • Αν Μ το μέσο του \overrightarrow{AB} και Ο ένα τυχαίο σημείο, τότε:

        \[2\overrightarrow{OM}=\overrightarrow{OA}+\overrightarrow{OB}\Longleftrightarrow \overrightarrow{OM}=\dfrac{\overrightarrow{OA}+\overrightarrow{OB}}{2}\]

    • Rendered by QuickLaTeX.com

  • Αν έχω ένα τυχαίο σημείο πάνω σ΄ ένα διάστημα πρέπει να αποδείξω, για να χρησιμοποιήσω την παρακάτω σχέση:
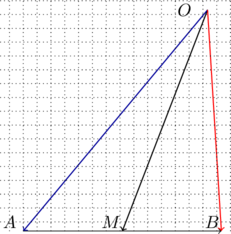
    Αν Μ ένα σημείο πάνω στο διάνυσμα \overrightarrow{AB} το οποίο χωρίζει ΑΒ σε λόγο λ. δηλαδή \overrightarrow{AM}=\grl \overrightarrow{MB}, \ \grl \neq 0, -1 \ \text{τότε} \ \overrightarrow{OM}=\dfrac{\overrightarrow{OA}+\grl \overrightarrow{OB}}{\grl +1}

    • Παράδειγμα.1
    Αν Μ ένα σημείο πάνω στο διάνυσμα \overrightarrow{AB} το οποίο χωρίζει ΑΒ σε λόγο λ. δηλαδή \overrightarrow{AM}=\grl \overrightarrow{MB}, \ \grl \neq 0, -1 \ \text{τότε να δείξετε ότι} \ \overrightarrow{OM}=\dfrac{\overrightarrow{OA}+\grl \overrightarrow{OB}}{\grl +1}

    Λύση

    dianlog

    Από το τρίγωνο ΟΑΜ έχουμε: \overrightarrow{OM}=\overrightarrow{OA}+\overrightarrow{AM} (1)

    Από το τρίγωνο ΟΜB έχουμε: \overrightarrow{OM}=\overrightarrow{OB}+\overrightarrow{BM}\Longleftrightarrow \grl \overrightarrow{OM}=\grl \overrightarrow{OB}+\grl \overrightarrow{BM} (2)

    Από (1)+(2) έχουμε: \overrightarrow{OM}+\grl \overrightarrow{OM}=\overrightarrow{OA}+\overrightarrow{AM}+\grl \overrightarrow{OB}+\grl \overrightarrow{BM} \ (3)

    Από την υπόθεση έχουμε ότι \overrightarrow{AM}=\grl \overrightarrow{MB}\Longleftrightarrow \overrightarrow{AM}=-\grl \overrightarrow{ΒΜ}\Longleftrightarrow \overrightarrow{AM}+\grl \overrightarrow{ΒΜ}=\overrightarrow{0} \ (4)

    Από (3), (4) έχουμε:

        \begin{align*} (3)\overset{(4)}{\Rightarrow} &\overrightarrow{OM}+\grl \overrightarrow{OM}= \overrightarrow{OA}+\grl \overrightarrow{OB} \Rightarrow \\\\ & (1+\grl)\overrightarrow{OM}=\overrightarrow{OA}+\grl \overrightarrow{OB} \Rightarrow \\\\ &\overrightarrow{OM}=\dfrac{\overrightarrow{OA}+\grl \overrightarrow{OB}}{\grl +1} \end{align*}

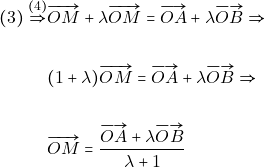
    Παράδειγμα.2.
    Αν ισχύει ότι: \overrightarrow{AB}+\overrightarrow{\grG A}=\overrightarrow{KB}+\overrightarrow{\grG\grL}, να δείξετε ότι τα σημεία Κ, Λ ταυτίζονται.

    Λύση

        \begin{align*} &\overrightarrow{AB}+\overrightarrow{\grG A}=\overrightarrow{KB}+\overrightarrow{\grG\grL} \Leftrightarrow \\\\ &\overrightarrow{AB}+\overrightarrow{\grG A}-\overrightarrow{KB}-\overrightarrow{\grG\grL}=\overrightarrow{0}\Leftrightarrow \\\\ & \overrightarrow{AB}-\overrightarrow{KB}+\overrightarrow{\grG A}-\overrightarrow{\grG\grL}=\overrightarrow{0}\Leftrightarrow \\\\ & \overrightarrow{AB}+\overrightarrow{BK}+\overrightarrow{\grG A}-\overrightarrow{\grG\grL}=\overrightarrow{0}\Leftrightarrow \\\\ & \overrightarrow{AK}+\overrightarrow{\grL A}=\overrightarrow{0}\Leftrightarrow \\\\ & \overrightarrow{AK}-\overrightarrow{A\grL }=\overrightarrow{0}\Leftrightarrow \\\\ & \overrightarrow{\grL K}=\overrightarrow{0} \end{align*}

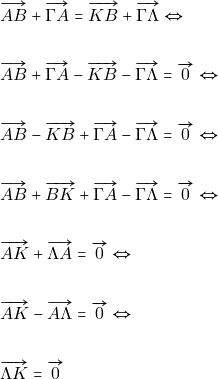
    Άρα Κ, Λ ταυτίζονται.

    Παράδειγμα.3
    Δίνεται τετράπλευρο ΑΒΓΔ και Κ, Λ τα μέσα των διαγωνίων ΑΓ και ΒΔ, να αποδείξετε ότι:

        \[\overrightarrow{A\grG}+\overrightarrow{\grG B}+\overrightarrow{\grG\grD}+\overrightarrow{A\grD}=4\overrightarrow{K\grL}\]

    Λύση

    Θεωρώ σημείο αναφοράς Ο και γράφω όλα τα διανύσματα στη σχέση που μου δίνεται ως διανυσματικές ακτίνες του Ο.

        \begin{align*} &\overrightarrow{A\grG}+\overrightarrow{\grG B}+\overrightarrow{\grG\grD}+\overrightarrow{A\grD} = \\\\ & \overrightarrow{O\grG}-\overrightarrow{OA}+\overrightarrow{O B}-\overrightarrow{O\grG}+\overrightarrow{O\grD}-\overrightarrow{O\grG}+\overrightarrow{O\grD}-\overrightarrow{OA}=\\\\ & 2\overrightarrow{O B}-2\overrightarrow{O\grG}+2\overrightarrow{O\grD}-2\overrightarrow{OA}=\\\\\ & 2(\overrightarrow{O B}+\overrightarrow{O\grD})-2(\overrightarrow{O\grD}-\overrightarrow{O\grG}) \, (1) \end{align*}

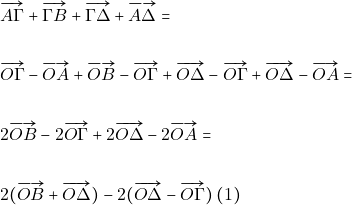
    Επειδή Κ μέσο του ΑΓ είναι: \overrightarrow{OA}+\overrightarrow{O\grG}=2\overrightarrow{OK}

    Επειδή Λ μέσο του ΒΔ είναι: \overrightarrow{OΒ}+\overrightarrow{O\grD}=2\overrightarrow{O\grL}

    Άρα από την (1) έχουμε:

        \begin{eqnarray*} \overrightarrow{A\grG}+\overrightarrow{\grG B}+\overrightarrow{\grG\grD}+\overrightarrow{A\grD} & = & 2(\overrightarrow{O B}+\overrightarrow{O\grD})-2(\overrightarrow{O\grD}-\overrightarrow{O\grG})\\\\ & = & 2 \cdot 2\overrightarrow{O\grL}-2\cdot 2\overrightarrow{OK} \\\\ & = & 4\overrightarrow{O\grL}-4\overrightarrow{OK} \\\\ & = & 4\overrightarrow{K\grL} \end{eqnarray*}

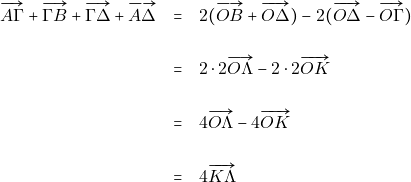
    Επιμέλεια: Γ. Αποστόλου Μαθηματικός. www.apgm.gr
    Άδεια Creative Commons
    Αυτή η εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή 4.0 Διεθνές .

    Αφήστε μια απάντηση

    Η ηλ. διεύθυνση σας δεν δημοσιεύεται. Τα υποχρεωτικά πεδία σημειώνονται με *

    Δεν είμαι Robot *