Δίνεται συνάρτηση ![]() παραγωγίσιμη στο
παραγωγίσιμη στο ![]() με
με ![]() της οποίας η γραφική παράσταση δεν διέρχεται απο την αρχή των αξόνων. Επιπλέον ισχύει
της οποίας η γραφική παράσταση δεν διέρχεται απο την αρχή των αξόνων. Επιπλέον ισχύει
![]()
i) Να βρείτε την τιμή ![]()
ii) Να αποδείξετε ότι η ![]() είναι παραγωγίσιμη σε κάθε
είναι παραγωγίσιμη σε κάθε ![]() και ισχύει
και ισχύει
![]()
Λύση
i) Αφου η σχέση ![]() ισχύει για κάθε
ισχύει για κάθε ![]() άρα θα ισχύει και για
άρα θα ισχύει και για ![]() οπότε προκύπτει ότι:
οπότε προκύπτει ότι:
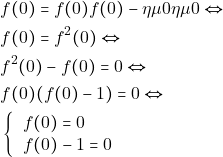
Επειδή η ![]() δεν διέρχεται από την αρχή των αξόνων άρα
δεν διέρχεται από την αρχή των αξόνων άρα ![]() .
.
έχουμε οτι ![]()
ii) Για να είναι η ![]() παραγωγίσιμη στο
παραγωγίσιμη στο ![]() θα πρέπει το όριο
θα πρέπει το όριο
![]()
να υπάρχει και να είναι πραγματικός αριθμός.
Επιπλέον έχουμε οτι η σχέση ![]() ισχύει για κάθε
ισχύει για κάθε ![]()
άρα θα ισχύει και για ![]() και
και ![]() οπότε προκύπτει ότι:
οπότε προκύπτει ότι:
![]()
Συνεπώς:
![]()
![]()
![]()
![]()
![]()
Απο υπόθεση έχουμε οτι ![]() δηλαδή
δηλαδή
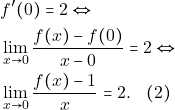
Τελικά απο (1)και (2) έχουμε:
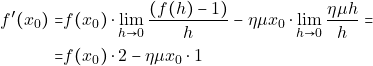
Επομένως η ![]() είναι παραγωγίσιμη σε κάθε
είναι παραγωγίσιμη σε κάθε ![]() και ισχύει:
και ισχύει:
![]()

Αυτή η εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή 4.0 Διεθνές .

Καλή η επιλογή και ενδιαφέρον θέμα!
Καλή συνέχεια!