Συνημίτονο γωνίας δύο διανυσμάτων
Θεωρούμε δύο διανύσματα  του επιπέδου
του επιπέδου
και έστω
Το συνημτονο της γωνίας που σχηματιζουν τα διανύσματα
που σχηματιζουν τα διανύσματα  δίνεται από τον τύπο:
δίνεται από τον τύπο:
και έστω
Το συνημτονο της γωνίας
![]()
ΑΠΟΔΕΙΞΗ
Θεωρούμε δύο διανύσματα ![]() του επιπέδου
του επιπέδου
και έστω ![]() η γωνία που σχηματίζουν.
η γωνία που σχηματίζουν.
Τότε από τον ορισμό του εσωτερικού γινομένου δύο διανυσμάτων έχουμε:
![]()
Λύνοντας ως προς ![]() προκύπτει ότι:
προκύπτει ότι:
![]()
Επειδή ![]() οπότε αν γνωρίζουμε το
οπότε αν γνωρίζουμε το ![]() μπορούμε να προσδιορίσουμε τη γωνία
μπορούμε να προσδιορίσουμε τη γωνία ![]()
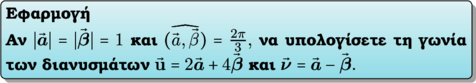
ΛΥΣΗ
Βρίσκουμε αρχικά ότι:
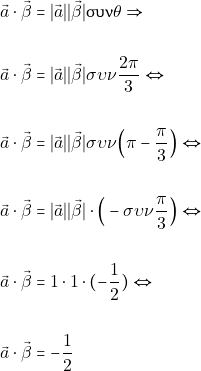
Αν ![]() είναι η γωνία των διανυσμάτων
είναι η γωνία των διανυσμάτων ![]() και
και ![]() τότε
τότε
![]()
`Ομως είναι:
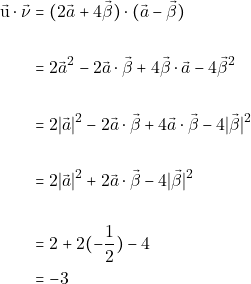
![]()
Επίσης επειδή: ![]()
Τότε θα ισχύει: ![]()
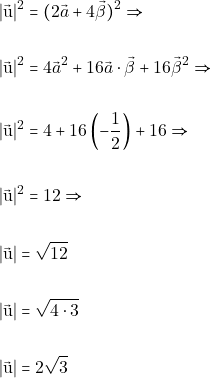
Τέλος είναι ![]()
οπότε θα ισχύει: ![]()
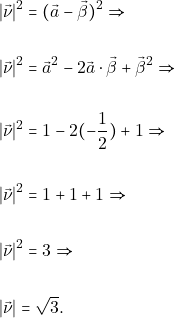
Επομένως είναι:
![]()
![]()
![]()
![]()
![]()
![]() άρα
άρα ![]()
Βιβλιογραφία:
Παπαδάκης εκδόσεις Σαββάλα.

Αυτή η εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή 4.0 Διεθνές .
