Έστω μια συνάρτηση ![]() η οποία είναι δύο φορές παραγωγίσιμη σε ένα διάστημα
η οποία είναι δύο φορές παραγωγίσιμη σε ένα διάστημα ![]()
Για να είναι η ![]() κυρτή (αντίστοιχα κοίλη) στο
κυρτή (αντίστοιχα κοίλη) στο ![]() αρκεί να ισχύει
αρκεί να ισχύει ![]() (αντίστοιχα
(αντίστοιχα ![]() ) για κάθε
) για κάθε ![]() και η ισότητα
και η ισότητα ![]() να ισχύει για διακεκριμένες τιμές του
να ισχύει για διακεκριμένες τιμές του ![]()
Παράδειγμα.
Δίνεται η συνάρτηση
![]()
Να βρείτε για ποιές τιμές του ![]() η συνάρτηση είναι κυρτή στο
η συνάρτηση είναι κυρτή στο ![]()
Λύση
Η ![]() είναι δύο φορές παραγωγίσιμη στο
είναι δύο φορές παραγωγίσιμη στο ![]()
Για κάθε ![]() είναι:
είναι:
![]()
Επίσης για κάθε ![]() είναι:
είναι:
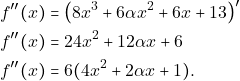
Για να είναι κυρτή στο ![]() πρέπει να ισχύει:
πρέπει να ισχύει:
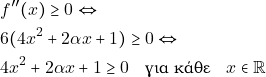
Άρα το τριώνυμο ![]() πρέπει να έχει:
πρέπει να έχει:
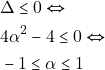
Βιβλιογραφία: Παπαδάκης, εκδόσεις Σαββάλα.

Αυτή η εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή 4.0 Διεθνές .
