Για τον υπολογισμό ορίων της μορφής ![]() τότε:
τότε:
- Θέτουμε
 οπότε
οπότε 
- Αν
 κοντά στο
κοντά στο  τότε
τότε 
Δηλαδή αντί να υπολογίσουμε το ![]() υπολογίζουμε το (πιθανόν) ευκολότερο
υπολογίζουμε το (πιθανόν) ευκολότερο ![]()
Παράδειγμα.1
Να υπολογίσετε το όριο ![]()
Λύση.
Επειδή ![]()
Το όριο γίνεται:
![Rendered by QuickLaTeX.com \[\orio{x}{0}{\dfrac{\hm 9x}{\hm 3x}}=\orio{x}{0}{\dfrac{\frac{\hm 9x}{x}}{\frac{\hm 3x}{x}}}=\orio{x}{0}{\dfrac{9\cdot\frac{\hm 9x}{9x}}{3\cdot\frac{\hm 3x}{3x}}}=\dfrac{\orio{x}{0}{9\cdot\frac{\hm 9x}{9x}}}{\orio{x}{0}{3\cdot\frac{\hm 3x}{3x}}}\]](https://study4maths.gr/wp-content/ql-cache/quicklatex.com-ff77cee6303dbbcfc5edeca52a264c72_l3.png)
Υπολογισμός του ![]()
Θέτουμε ![]() οπότε έχουμε:
οπότε έχουμε:
![]()
Δηλαδή όταν το ![]() τότε το
τότε το ![]() δηλαδή
δηλαδή ![]() άρα έχουμε:
άρα έχουμε:
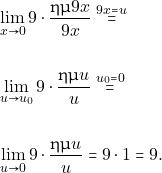
Υπολογισμός του ![]()
Όμοια θέτουμε ![]() οπότε έχουμε:
οπότε έχουμε:
![]()
Δηλαδή όταν το ![]() τότε το
τότε το ![]() δηλαδή
δηλαδή ![]() άρα έχουμε:
άρα έχουμε:
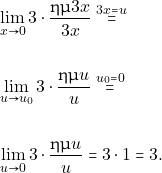
Άρα το όριο είναι ίσο με:
![]()
Παράδειγμα.2
Να υπολογιστεί το όριο ![]()
Λύση.
Επειδή ![]()
για να άρουμε την απροσδιοριστία χρησιμοποιούμε την ιδιότητα
![]()
Οπότε έχουμε:
![]()
Θέτουμε:
![]()
Είναι:
![]()
Δηλαδή όταν το ![]() τότε το
τότε το ![]() δηλαδή
δηλαδή ![]() άρα έχουμε:
άρα έχουμε:
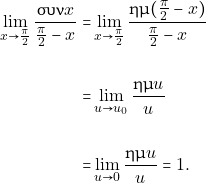
Βιβλιογραφία: Παπαδάκης, εκδόσεις Σαββάλα. Στεργίου – Νάκης, εκδόσεις Σαββάλα.

Αυτή η εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή 4.0 Διεθνές .
