Γ Λυκείου,ΣΥΝΑΡΤΗΣΗ 1-1

ΣΥΝΑΡΤΗΣΕΙΣ 1-1 ΚΑΙ ΕΞΙΣΩΣΕΙΣ

Σχολιάστε
Print Friendly, PDF & Email

ΣΥΝΑΡΤΗΣΕΙΣ 1-1 ΚΑΙ ΕΞΙΣΩΣΕΙΣ

Μια εξίσωση που δεν λύνεται με κάποια γνωστή μέθοδο, μπορεί να λυθεί ως εξής:

  • Μεταφέρουμε όλους τους όρους στο πρώτο μέλος.
  • Θέτουμε το πρώτο μέλος ίσο με f(x), οπότε η εξίσωση έχει τη μορφή f(x)=0
  • Αποδεικνύουμε ότι η f είναι 1-1.
  • Βρίσκουμε με δοκιμές μία ρίζα x_{0} της εξίσωσης f(x)=0
  • Η εξίσωση γίνεται

        \begin{align*} &f(x)=0 \Leftrightarrow\\ &f(x)=f(x_{0}) \stackrel{1-1}{\Leftrightarrow} \\ &x=x_{0} \end{align*}

Στην περίπτωση η παράσταση στο πρώτο μέλος δεν οριζει μια προφανή συνάρτηση 1-1

  • Γράφουμε την εξίσωση με κατάλληλες μετακινήσεις όρων απο το ένα μέλος στο άλλο ωστε να εμφανίζεται μια ομοιότητα και στα δύο μέλη.
  • Θεωρόυμε μια γενικότερη συνάρτηση f που εκφράζει τη δομή των μελών, ώστε η εξίσωση να παίρνει τη μορφή

        \[f\big(g(x)\big) =f\big(h(x)\big).\]

Αποδεικνύουμε ότι η συνάρτηση f είναι 1-1 οπότε η προηγούμενη εξίσωση, ισοδύναμα καταλήγει στην απλούστερη εξίσωση:

    \[g(x)=h(x).\]

Παράδειγμα.1
Να λυθεί η εξίσωση e^x=1-x^7.
Λύση

Έχουμε e^x=1-x^7\Leftrightarrow e^{x}+x^{7}-1 =0.
Θεωρούμε την συνάρτηση:

    \[f(x)= e^{x}+x^{7}-1, \quad x\in A_{f}=\mathbb{R}.\]

Αποδεικνύουμε ότι η f είναι 1-1.
Έστω x_{1},x_{2}\in A_{f} με x_{1}\neq x_{2} τότε

    \begin{align*} x_{1}\neq x_{2}\Rightarrow e^{x_{1}}\neq e^{x_{2}}. \quad (1) \end{align*}

Επίσης

    \begin{align*} x_{1}&\neq x_{2}\Rightarrow \\ x_{1}^{7}&\neq x_{2}^{7}\Rightarrow\\ x_{1}^{7}-1 & \neq x_{2}^{7}-1. \quad (2) \end{align*}

Προσθέτουμε τις (1) και (2) και έχουμε:

    \[ \left\{ \begin{tabular}{ll} $e^{x_{1}}\neq e^{x_{2}}$ \\ $x_{1}^{7}-1\neq x_{2}^{7}-1$ \end{tabular} \right.\overset{+}{\Rightarrow}\]

e^{x_{1}}+x_{1}^{7}-1\neq e^{x_{2}}+x_{2}^{7}-1\Rightarrow f(x_{1})\neq f(x_{2}).
Άρα για την συνάρτηση f ικανοποιούνται οι απαιτήσεις του ορισμού της 1-1 συνάρτησης
δηλ.η f:A \to \mathbb{R} λέγεται συνάρτηση 1-1, όταν για οποιαδήποτε x_{1}, x_{2} \in A ισχύει η συνεπαγωγή:

    \[x_{1}\neq x_{2} \Rightarrow f(x_{1}) \neq f(x_{2}).\]

άρα θα ισχύει και

    \[f(x_{1}) = f(x_{2})\Rightarrow x_{1}= x_{2}.\]

οπότε έχουμε

    \begin{align*} &e^x=1-x^7\Leftrightarrow\\ &e^{x}+x^{7}-1 =0 \Leftrightarrow\\ &f(x) =0 \end{align*}

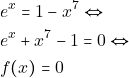
Παρατηρούμε ότι έχουμε μια προφανή ρίζα την x=0 αφού:
f(0)=e^0-1-x^7=1-1-0 = 0
άρα

    \begin{align*} &f(x) =f(0)\overset{1-1}{\Leftrightarrow}\\ &x=0. \end{align*}

Β.ΤΡΟΠΟΣ.
Η συγκεκριμένη εξίσωση μπορεί να λυθεί και με τη χρήση της μονοτονίας συνάρτησης.
Η εξίσωση γράφεται ισοδύναμα: e^x-1+x^7=0
Θέτουμε: f(x)=e^x-1+x^7 με A_{f}=\mathbb{R}
Οπότε η εξίσωση γίνεται: f(x)=0
Θα μελετήσουμε την f ως προς την μονοτονία.
Έστω x_{1}, x_{2} \in A_{f}=\mathbb{R} με x_{1}< x_{2}.
Έχουμε:

x_{1}< x_{2} \Leftrightarrow e^{x_{1}}< e^{x_{2}}
και

x_{1}< x_{2} \Leftrightarrow x_{1}^7< x_{2}^7
Προσθέτουμε τις παραπάνω ανισώσεις και έχουμε:

    \[e^{x_{1}}-1+x_{1}^7<e^{x_{2}}-1+x_{2}^7 \Leftrightarrow\\ f(x_{1})< f(x_{2})\]

Άρα η συνάρτηση f είναι γνησίως μονότονη ως γνησίως αύξουσα, οπότε είναι και 1-1.
Παρατηρούμε ότι έχουμε μια προφανή ρίζα την x=0 αφού:
f(0)=e^0-1-x^7 =1-1-0 = 0
Έτσι η εξίσωση f(x)=0 γίνεται:
f(x)=0 \Leftrightarrow f(x)=f(0) \stackrel{1-1}{\Leftrightarrow} x=0

Παράδειγμα.2
Δίνεται η συνάρτηση f(x)=x+\ln x.

i)Να αποδείξετε ότι η f είναι 1-1.
ii) Να λύσετε την εξίσωση \ln\dfrac{\sqrt{x}+1}{x^2+1}=x^2-\sqrt{x}

Λύση

i) Η συνάρτηση f(x)=x+\ln x ορίζεται όταν x>0.
Άρα το πεδίο ορισμού της f είναι το σύνολο A_{f}=(0, +\infty)
Θα μελετήσουμε την f ως προς την μονοτονία.
Έστω x_{1}, x_{2} \in A_{f}=(0, +\infty) με x_{1}< x_{2}. Έχουμε:
x_{1}< x_{2} \Leftrightarrow \ln x_{1}< \ln x_{2}
και
x_{1}< x_{2}

Προσθέτουμε τις παραπάνω ανισώσεις και έχουμε:

    \[x_{1}+\ln x_{1}< x_{2}+ \ln x_{2} \Leftrightarrow f(x_{1})< f(x_{2})\]

Άρα η συνάρτηση f είναι γνησίως αύξουσα, οπότε είναι και 1-1.
ii) Η εξίσωση γίνεται:

    \begin{align*} &\ln\dfrac{\sqrt{x}+1}{x^2+1}=x^2-\sqrt{x} \Leftrightarrow \\\\ &\ln(\sqrt{x}+1)-\ln(x^2+1)=x^2-\sqrt{x}\Leftrightarrow \\\\ & \sqrt{x}+\ln(\sqrt{x}+1)=x^2+\ln(x^2+1)\Leftrightarrow \\\\ &\sqrt{x}+1+\ln(\sqrt{x}+1)=x^2+1+\ln(x^2+1)\Leftrightarrow\\\\ &f(\sqrt{x}+1)=f(x^2+1) \stackrel{1-1}{\Leftrightarrow}\\\\ &\sqrt{x}+1=x^2+1 \Leftrightarrow \sqrt{x}=x^2\Leftrightarrow x=x^4 \Leftrightarrow\\\\ &x^4-x=0 \Leftrightarrow x(x^3-1)=0 \Leftrightarrow \\\\ & \left\{ \begin{tabular}{ll} $ x=0$ \\ $x^3-1=0$ \end{tabular} \right. \Leftrightarrow \end{align*}

x=0 ή x=1.

Βιβλιογραφία: Παπαδάκης, εκδόσεις Σαββάλα. Δ.Α.Παπακωνσταντίνου, αυτοέκδοση.
Άδεια Creative Commons
Αυτή η εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή 4.0 Διεθνές .

Αφήστε μια απάντηση

Η ηλ. διεύθυνση σας δεν δημοσιεύεται. Τα υποχρεωτικά πεδία σημειώνονται με *

Δεν είμαι Robot *