ΣΥΝΘΕΣΗ ΣΥΝΑΡΤΗΣΕΩΝ
Έστω ![]() και
και ![]() δύο συναρτήσεις με πεδία ορισμού
δύο συναρτήσεις με πεδία ορισμού ![]() και
και ![]() αντίστοιχα. Αν ισχύει
αντίστοιχα. Αν ισχύει ![]() , τότε ονομάζουμε σύνθεση της
, τότε ονομάζουμε σύνθεση της ![]() με τη
με τη ![]() και τη συμβολίζουμε με
και τη συμβολίζουμε με ![]() τη συνάρτηση που έχει:
τη συνάρτηση που έχει:
- Πεδίο ορισμού το σύνολο

- Και τύπο

Παράδειγμα.1
Δίνονται οι συναρτήσεις ![]() Να βρείτε τις συναρτήσεις:\quad
Να βρείτε τις συναρτήσεις:\quad
i) ![]()
ii) ![]()
Λύση
Αρχικά θα βρούμε τα πεδία ορισμού των συναρτήσεων ![]() και
και ![]()
Η συνάρτηση ![]() ορίζεται όταν:
ορίζεται όταν: ![]()
Άρα το πεδίο ορισμού της ![]() είναι το σύνολο
είναι το σύνολο ![]()
Η συνάρτηση ![]() ορίζεται όταν για κάθε
ορίζεται όταν για κάθε ![]()
Άρα το πεδίο ορισμού της ![]() είναι το σύνολο
είναι το σύνολο ![]()
i)Για να βρούμε την συνάρτηση ![]() πρέπει να υπολογίσουμε το πεδίο ορισμού της
πρέπει να υπολογίσουμε το πεδίο ορισμού της ![]() και τον αλγεβρικό της, τύπό.
και τον αλγεβρικό της, τύπό.
Έχουμε:
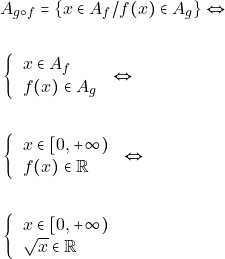
Επειδή ![]() έχουμε μόνο
έχουμε μόνο ![]() δηλαδή,
δηλαδή, ![]()
Αλγεβρικός τύπος της ![]() με
με ![]()
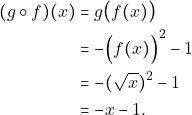
Τελικά ![]()
ii)Για να βρούμε την συνάρτηση ![]() πρέπει να υπολογίσουμε το πεδίο ορισμού της
πρέπει να υπολογίσουμε το πεδίο ορισμού της ![]() και τον αλγεβρικό της, τύπό.
και τον αλγεβρικό της, τύπό.
Έχουμε:
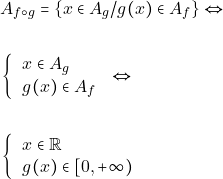
Επειδή ![]() έχουμε μόνο
έχουμε μόνο ![]() δηλαδή
δηλαδή
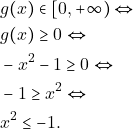
Το οποίο είναι αδύνατο άρα η ![]() δεν ορίζεται.
δεν ορίζεται.
Βιβλιογραφία: Παπαδάκης, εκδόσεις Σαββάλα

Αυτή η εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή 4.0 Διεθνές .
