Δίνεται συνάρτηση ![]() παραγωγίσιμη στο
παραγωγίσιμη στο ![]() για την οποία ισχύει:
για την οποία ισχύει:
![]() και
και ![]()
Να βρείτε τις τιμές ![]() και
και ![]()
Λύση
Αφού η ![]() είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο ![]() ισχύει ότι:
ισχύει ότι:
![]()
Από υπόθεση έχουμε ![]()
για να αξιοποιήσουμε την σχέση (1) θα προσθαφαιρέσουμε στον αριθμητή το ![]() και έχουμε:
και έχουμε:
![]()
![]()
![]()
![]()
![]()
Επίσης απο υπόθεση έχουμε ότι:
![]()
για να αξιοποιήσουμε την σχέση (1), αυτή τη φορά, θα προσθαφαιρέσουμε στον αριθμητή το ![]() και έχουμε:
και έχουμε:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Επομένως από τις σχέσεις ![]() και
και ![]() έχουμε:
έχουμε:
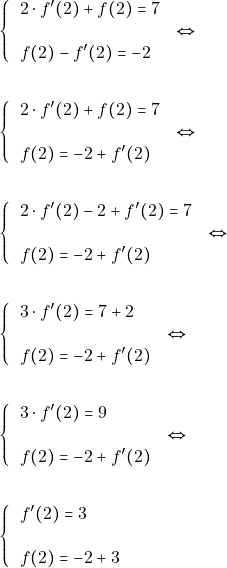
Τελικά ![]() και
και ![]()
Βιβλιογραφία: Παπαδάκης εκδόσεις Σαββάλα.

Αυτή η εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή 4.0 Διεθνές .
